Plasticity of Mohr-Coulomb with apex-smoothing#
This tutorial aims to demonstrate how modern automatic algorithmic
differentiation (AD) techniques may be used to define a complex constitutive
model demanding a lot of by-hand differentiation. In particular, we implement
the non-associative plasticity model of Mohr-Coulomb with apex-smoothing applied
to a slope stability problem for soil. We use the
JAX package to define constitutive
relations including the differentiation of certain terms and
FEMExternalOperator class to incorporate this model into a weak formulation
within UFL.
The tutorial is based on the limit analysis within semi-definite programming framework, where the plasticity model was replaced by the MFront/TFEL implementation of the Mohr-Coulomb elastoplastic model with apex smoothing.
Problem formulation#
We solve a slope stability problem of a soil domain \(\Omega\) represented by a rectangle \([0; L] \times [0; W]\) with homogeneous Dirichlet boundary conditions for the displacement field \(\boldsymbol{u} = \boldsymbol{0}\) on the right side \(x = L\) and the bottom one \(z = 0\). The loading consists of a gravitational body force \(\boldsymbol{q}=[0, -\gamma]^T\) with \(\gamma\) being the soil self-weight. The solution of the problem is to find the collapse load \(q_\text{lim}\), for which we know an analytical solution in the case of the standard Mohr-Coulomb model without smoothing under plane strain assumption for associative plastic law [Chen and Liu, 1990]. Here we follow the same Mandel-Voigt notation as in the von Mises plasticity tutorial.
If \(V\) is a functional space of admissible displacement fields, then we can write out a weak formulation of the problem:
Find \(\boldsymbol{u} \in V\) such that
\[
F(\boldsymbol{u}; \boldsymbol{v}) = \int\limits_\Omega
\boldsymbol{\sigma}(\boldsymbol{u}) \cdot
\boldsymbol{\varepsilon}(\boldsymbol{v}) \, \mathrm{d}\boldsymbol{x} -
\int\limits_\Omega \boldsymbol{q} \cdot \boldsymbol{v} \, \mathrm{d}\boldsymbol{x} = \boldsymbol{0}, \quad
\forall \boldsymbol{v} \in V,
\]
where \(\boldsymbol{\sigma}\) is an external operator representing the stress tensor.
Note
Although the tutorial shows the implementation of the Mohr-Coulomb model, it is quite general to be adapted to a wide rage of plasticity models that may be defined through a yield surface and a plastic potential.
Implementation#
Preamble#
from functools import partial
from mpi4py import MPI
from petsc4py import PETSc
import jax
import jax.lax
import jax.numpy as jnp
import matplotlib.cm as cm
import matplotlib.colors as mcolors
import matplotlib.pyplot as plt
import numpy as np
from mpltools import annotation # for slope markers
from utilities import assemble_residual_with_callback, find_cell_by_point
import basix
import ufl
from dolfinx import default_scalar_type, fem, mesh
from dolfinx.fem.petsc import NonlinearProblem
from dolfinx_external_operator import (
FEMExternalOperator,
evaluate_external_operators,
evaluate_operands,
replace_external_operators,
)
jax.config.update("jax_enable_x64", True)
Here we define geometrical and material parameters of the problem as well as some useful constants.
E = 6778 # [MPa] Young modulus
nu = 0.25 # [-] Poisson ratio
c = 3.45 # [MPa] cohesion
phi = 30 * np.pi / 180 # [rad] friction angle
psi = 30 * np.pi / 180 # [rad] dilatancy angle
theta_T = 26 * np.pi / 180 # [rad] transition angle as defined by Abbo and Sloan
a = 0.26 * c / np.tan(phi) # [MPa] tension cuff-off parameter
L, H = (1.2, 1.0)
Nx, Ny = (25, 25)
gamma = 1.0
domain = mesh.create_rectangle(MPI.COMM_WORLD, [np.array([0, 0]), np.array([L, H])], [Nx, Ny])
k_u = 2
gdim = domain.topology.dim
V = fem.functionspace(domain, ("Lagrange", k_u, (gdim,)))
# Boundary conditions
def on_right(x):
return np.isclose(x[0], L)
def on_bottom(x):
return np.isclose(x[1], 0.0)
bottom_dofs = fem.locate_dofs_geometrical(V, on_bottom)
right_dofs = fem.locate_dofs_geometrical(V, on_right)
bcs = [
fem.dirichletbc(np.array([0.0, 0.0], dtype=PETSc.ScalarType), bottom_dofs, V),
fem.dirichletbc(np.array([0.0, 0.0], dtype=PETSc.ScalarType), right_dofs, V),
]
def epsilon(v):
grad_v = ufl.grad(v)
return ufl.as_vector(
[
grad_v[0, 0],
grad_v[1, 1],
0.0,
np.sqrt(2.0) * 0.5 * (grad_v[0, 1] + grad_v[1, 0]),
]
)
k_stress = 2 * (k_u - 1)
dx = ufl.Measure(
"dx",
domain=domain,
metadata={"quadrature_degree": k_stress, "quadrature_scheme": "default"},
)
stress_dim = 2 * gdim
S_element = basix.ufl.quadrature_element(domain.topology.cell_name(), degree=k_stress, value_shape=(stress_dim,))
S = fem.functionspace(domain, S_element)
Du = fem.Function(V, name="Du")
u = fem.Function(V, name="Total_displacement")
du = fem.Function(V, name="du")
v = ufl.TestFunction(V)
sigma = FEMExternalOperator(epsilon(Du), function_space=S)
sigma_n = fem.Function(S, name="sigma_n")
Defining plasticity model and external operator#
The constitutive model of the soil is described by a non-associative plasticity law without hardening that is defined by the Mohr-Coulomb yield surface \(f\) and the plastic potential \(g\). Both quantities may be expressed through the following function \(h\)
\[\begin{align*}
& h(\boldsymbol{\sigma}, \alpha) =
\frac{I_1(\boldsymbol{\sigma})}{3}\sin\alpha +
\sqrt{J_2(\boldsymbol{\sigma}) K^2(\alpha) + a^2(\alpha)\sin^2\alpha} -
c\cos\alpha, \\
& f(\boldsymbol{\sigma}) = h(\boldsymbol{\sigma}, \phi), \\
& g(\boldsymbol{\sigma}) = h(\boldsymbol{\sigma}, \psi),
\end{align*}\]
where \(\phi\) and \(\psi\) are friction and dilatancy angles, \(c\) is a cohesion, \(I_1(\boldsymbol{\sigma}) = \mathrm{tr} \boldsymbol{\sigma}\) is the first invariant of the stress tensor and \(J_2(\boldsymbol{\sigma}) = \frac{1}{2}\boldsymbol{s} \cdot \boldsymbol{s}\) is the second invariant of the deviatoric part of the stress tensor. The expression of the coefficient \(K(\alpha)\) may be found in the MFront/TFEL implementation of this plastic model.
During the plastic loading the stress-strain state of the solid must satisfy the following system of nonlinear equations
(5)#\[\begin{split} \begin{cases}
\boldsymbol{r}_{g}(\boldsymbol{\sigma}_{n+1}, \Delta\lambda) =
\boldsymbol{\sigma}_{n+1} - \boldsymbol{\sigma}_n -
\boldsymbol{C} \cdot (\Delta\boldsymbol{\varepsilon} - \Delta\lambda
\frac{\mathrm{d} g}{\mathrm{d}\boldsymbol{\sigma}}(\boldsymbol{\sigma_{n+1}})) =
\boldsymbol{0}, \\
r_f(\boldsymbol{\sigma}_{n+1}) = f(\boldsymbol{\sigma}_{n+1}) = 0,
\end{cases}\end{split}\]
where \(\Delta\) is associated with increments of a quantity between the next loading step \(n + 1\) and the current loading step \(n\).
By introducing the residual vector \(\boldsymbol{r} = [\boldsymbol{r}_{g}^T, r_f]^T\) and its argument vector \(\boldsymbol{y}_{n+1} = [\boldsymbol{\sigma}_{n+1}^T, \Delta\lambda]^T\), we obtain the following nonlinear constitutive equation:
\[
\boldsymbol{r}(\boldsymbol{y}_{n+1}) = \boldsymbol{0}.
\]
To solve this equation we apply the Newton method and introduce the local Jacobian of the residual vector \(\boldsymbol{j} := \frac{\mathrm{d} \boldsymbol{r}}{\mathrm{d} \boldsymbol{y}}\). Thus we solve the following linear system at each quadrature point for the plastic phase
\[\begin{split}
\begin{cases}
\boldsymbol{j}(\boldsymbol{y}_{n})\boldsymbol{t} = -
\boldsymbol{r}(\boldsymbol{y}_{n}), \\
\boldsymbol{x}_{n+1} = \boldsymbol{x}_n + \boldsymbol{t}.
\end{cases}
\end{split}\]
During the elastic loading, we consider a trivial system of equations
(6)#\[\begin{split}
\begin{cases}
\boldsymbol{\sigma}_{n+1} = \boldsymbol{\sigma}_n +
\boldsymbol{C} \cdot \Delta\boldsymbol{\varepsilon}, \\ \Delta\lambda = 0.
\end{cases}
\end{split}\]
The algorithm solving the systems (5)–(6) is called the return-mapping procedure and the solution defines the return-mapping correction of the stress tensor. By implementation of the external operator \(\boldsymbol{\sigma}\) we mean the implementation of this algorithmic procedure.
The automatic differentiation tools of the JAX library are applied to calculate the three distinct derivatives:
\(\frac{\mathrm{d} g}{\mathrm{d}\boldsymbol{\sigma}}\) - derivative of the plastic potential \(g\),
\(j = \frac{\mathrm{d} \boldsymbol{r}}{\mathrm{d} \boldsymbol{y}}\) - derivative of the local residual \(\boldsymbol{r}\),
\(\boldsymbol{C}_\text{tang} = \frac{\mathrm{d}\boldsymbol{\sigma}}{\mathrm{d}\boldsymbol{\varepsilon}}\) - stress tensor derivative or consistent tangent moduli.
Defining yield surface and plastic potential#
First of all, we define supplementary functions that help us to express the
yield surface \(f\) and the plastic potential \(g\). In the following definitions,
we use built-in functions of the JAX package, in particular, the conditional
primitive jax.lax.cond. It is necessary for the correct work of the AD tool
and just-in-time compilation. For more details, please, visit the JAX
documentation.
def J3(s):
return s[2] * (s[0] * s[1] - s[3] * s[3] / 2.0)
def J2(s):
return 0.5 * jnp.vdot(s, s)
def theta(s):
J2_ = J2(s)
arg = -(3.0 * np.sqrt(3.0) * J3(s)) / (2.0 * jnp.sqrt(J2_ * J2_ * J2_))
arg = jnp.clip(arg, -1.0, 1.0)
theta = 1.0 / 3.0 * jnp.arcsin(arg)
return theta
def sign(x):
return jax.lax.cond(x < 0.0, lambda x: -1, lambda x: 1, x)
def coeff1(theta, angle):
return np.cos(theta_T) - (1.0 / np.sqrt(3.0)) * np.sin(angle) * np.sin(theta_T)
def coeff2(theta, angle):
return sign(theta) * np.sin(theta_T) + (1.0 / np.sqrt(3.0)) * np.sin(angle) * np.cos(theta_T)
coeff3 = 18.0 * np.cos(3.0 * theta_T) * np.cos(3.0 * theta_T) * np.cos(3.0 * theta_T)
def C(theta, angle):
return (
-np.cos(3.0 * theta_T) * coeff1(theta, angle) - 3.0 * sign(theta) * np.sin(3.0 * theta_T) * coeff2(theta, angle)
) / coeff3
def B(theta, angle):
return (
sign(theta) * np.sin(6.0 * theta_T) * coeff1(theta, angle) - 6.0 * np.cos(6.0 * theta_T) * coeff2(theta, angle)
) / coeff3
def A(theta, angle):
return (
-(1.0 / np.sqrt(3.0)) * np.sin(angle) * sign(theta) * np.sin(theta_T)
- B(theta, angle) * sign(theta) * np.sin(3 * theta_T)
- C(theta, angle) * np.sin(3.0 * theta_T) * np.sin(3.0 * theta_T)
+ np.cos(theta_T)
)
def K(theta, angle):
def K_false(theta):
return jnp.cos(theta) - (1.0 / np.sqrt(3.0)) * np.sin(angle) * jnp.sin(theta)
def K_true(theta):
return (
A(theta, angle)
+ B(theta, angle) * jnp.sin(3.0 * theta)
+ C(theta, angle) * jnp.sin(3.0 * theta) * jnp.sin(3.0 * theta)
)
return jax.lax.cond(jnp.abs(theta) > theta_T, K_true, K_false, theta)
def a_g(angle):
return a * np.tan(phi) / np.tan(angle)
dev = np.array(
[
[2.0 / 3.0, -1.0 / 3.0, -1.0 / 3.0, 0.0],
[-1.0 / 3.0, 2.0 / 3.0, -1.0 / 3.0, 0.0],
[-1.0 / 3.0, -1.0 / 3.0, 2.0 / 3.0, 0.0],
[0.0, 0.0, 0.0, 1.0],
],
dtype=PETSc.ScalarType,
)
tr = np.array([1.0, 1.0, 1.0, 0.0], dtype=PETSc.ScalarType)
def surface(sigma_local, angle):
s = dev @ sigma_local
I1 = tr @ sigma_local
theta_ = theta(s)
return (
(I1 / 3.0 * np.sin(angle))
+ jnp.sqrt(
J2(s) * K(theta_, angle) * K(theta_, angle) + a_g(angle) * a_g(angle) * np.sin(angle) * np.sin(angle)
)
- c * np.cos(angle)
)
By picking up an appropriate angle we define the yield surface \(f\) and the plastic potential \(g\).
def f(sigma_local):
return surface(sigma_local, phi)
def g(sigma_local):
return surface(sigma_local, psi)
dgdsigma = jax.jacfwd(g)
Solving constitutive equations#
In this section, we define the constitutive model by solving the systems
(5)–(6). They must be solved at each Gauss point, so we
apply the Newton method, implement the whole algorithm locally and then
vectorize the final result using jax.vmap.
In the following cell, we define locally the residual \(\boldsymbol{r}\) and
its Jacobian drdy.
lmbda = E * nu / ((1.0 + nu) * (1.0 - 2.0 * nu))
mu = E / (2.0 * (1.0 + nu))
C_elas = np.array(
[
[lmbda + 2 * mu, lmbda, lmbda, 0],
[lmbda, lmbda + 2 * mu, lmbda, 0],
[lmbda, lmbda, lmbda + 2 * mu, 0],
[0, 0, 0, 2 * mu],
],
dtype=PETSc.ScalarType,
)
S_elas = np.linalg.inv(C_elas)
ZERO_VECTOR = np.zeros(stress_dim, dtype=PETSc.ScalarType)
def deps_p(sigma_local, dlambda, deps_local, sigma_n_local):
sigma_elas_local = sigma_n_local + C_elas @ deps_local
yielding = f(sigma_elas_local)
def deps_p_elastic(sigma_local, dlambda):
return ZERO_VECTOR
def deps_p_plastic(sigma_local, dlambda):
return dlambda * dgdsigma(sigma_local)
return jax.lax.cond(yielding <= 0.0, deps_p_elastic, deps_p_plastic, sigma_local, dlambda)
def r_g(sigma_local, dlambda, deps_local, sigma_n_local):
deps_p_local = deps_p(sigma_local, dlambda, deps_local, sigma_n_local)
return sigma_local - sigma_n_local - C_elas @ (deps_local - deps_p_local)
def r_f(sigma_local, dlambda, deps_local, sigma_n_local):
sigma_elas_local = sigma_n_local + C_elas @ deps_local
yielding = f(sigma_elas_local)
def r_f_elastic(sigma_local, dlambda):
return dlambda
def r_f_plastic(sigma_local, dlambda):
return f(sigma_local)
return jax.lax.cond(yielding <= 0.0, r_f_elastic, r_f_plastic, sigma_local, dlambda)
def r(y_local, deps_local, sigma_n_local):
sigma_local = y_local[:stress_dim]
dlambda_local = y_local[-1]
res_g = r_g(sigma_local, dlambda_local, deps_local, sigma_n_local)
res_f = r_f(sigma_local, dlambda_local, deps_local, sigma_n_local)
res = jnp.c_["0,1,-1", res_g, res_f] # concatenates an array and a scalar
return res
drdy = jax.jacfwd(r)
Then we define the function return_mapping that implements the
return-mapping algorithm numerically via the Newton method.
Nitermax, tol = 200, 1e-8
ZERO_SCALAR = np.array([0.0])
def return_mapping(deps_local, sigma_n_local):
"""Performs the return-mapping procedure.
It solves elastoplastic constitutive equations numerically by applying the
Newton method in a single Gauss point. The Newton loop is implement via
`jax.lax.while_loop`.
The function returns `sigma_local` two times to reuse its values after
differentiation, i.e. as once we apply
`jax.jacfwd(return_mapping, has_aux=True)` the ouput function will
have an output of
`(C_tang_local, (sigma_local, niter_total, yielding, norm_res, dlambda))`.
Returns:
sigma_local: The stress at the current Gauss point.
niter_total: The total number of iterations.
yielding: The value of the yield function.
norm_res: The norm of the residuals.
dlambda: The value of the plastic multiplier.
"""
niter = 0
dlambda = ZERO_SCALAR
sigma_local = sigma_n_local
y_local = jnp.concatenate([sigma_local, dlambda])
res = r(y_local, deps_local, sigma_n_local)
norm_res0 = jnp.linalg.norm(res)
def cond_fun(state):
norm_res, niter, _ = state
return jnp.logical_and(norm_res / norm_res0 > tol, niter < Nitermax)
def body_fun(state):
norm_res, niter, history = state
y_local, deps_local, sigma_n_local, res = history
j = drdy(y_local, deps_local, sigma_n_local)
j_inv_vp = jnp.linalg.solve(j, -res)
y_local = y_local + j_inv_vp
res = r(y_local, deps_local, sigma_n_local)
norm_res = jnp.linalg.norm(res)
history = y_local, deps_local, sigma_n_local, res
niter += 1
return (norm_res, niter, history)
history = (y_local, deps_local, sigma_n_local, res)
norm_res, niter_total, y_local = jax.lax.while_loop(cond_fun, body_fun, (norm_res0, niter, history))
sigma_local = y_local[0][:stress_dim]
dlambda = y_local[0][-1]
sigma_elas_local = C_elas @ deps_local
yielding = f(sigma_n_local + sigma_elas_local)
return sigma_local, (sigma_local, niter_total, yielding, norm_res, dlambda)
Consistent tangent stiffness matrix#
Not only is the automatic differentiation able to compute the derivative of a mathematical expression but also a numerical algorithm. For instance, AD can calculate the derivative of the function performing return-mapping with respect to its output, the stress tensor \(\boldsymbol{\sigma}\). In the context of the consistent tangent moduli \(\boldsymbol{C}_\text{tang}\), this feature becomes very useful, as there is no need to write an additional program computing the stress derivative.
JAX’s AD tool permits taking the derivative of the function return_mapping,
which is factually the while loop. The derivative is taken with respect to the
first output and the remaining outputs are used as auxiliary data. Thus, the
derivative dsigma_ddeps returns both values of the consistent tangent moduli
and the stress tensor, so there is no need in a supplementary computation of the
stress tensor.
dsigma_ddeps = jax.jacfwd(return_mapping, has_aux=True)
Defining external operator#
Once we define the function dsigma_ddeps, which evaluates both the
external operator and its derivative locally, we can simply vectorize it and
define the final implementation of the external operator derivative.
Note
The function dsigma_ddeps containing a while_loop is designed to be called
at a single Gauss point that’s why we need to vectorize it for the all points
of our functional space S. For this purpose we use the vmap function of JAX.
It creates another while_loop, which terminates only when all mapped loops
terminate. Find further details in this
discussion.
dsigma_ddeps_vec = jax.jit(jax.vmap(dsigma_ddeps, in_axes=(0, 0)))
def C_tang_impl(deps):
deps_ = deps.reshape((-1, stress_dim))
sigma_n_ = sigma_n.x.array.reshape((-1, stress_dim))
(C_tang_global, state) = dsigma_ddeps_vec(deps_, sigma_n_)
sigma_global, niter, yielding, norm_res, _dlambda = state
unique_iters, counts = jnp.unique(niter, return_counts=True)
if MPI.COMM_WORLD.rank == 0:
print("\tInner Newton summary:")
print(f"\t\tUnique number of iterations: {unique_iters}")
print(f"\t\tCounts of unique number of iterations: {counts}")
print(f"\t\tMaximum f: {jnp.max(yielding)}")
print(f"\t\tMaximum residual: {jnp.max(norm_res)}")
return C_tang_global.reshape(-1), sigma_global.reshape(-1)
Similarly to the von Mises example, we do not implement explicitly the evaluation of the external operator. Instead, we obtain its values during the evaluation of its derivative and then update the values of the operator in the main Newton loop.
def sigma_external(derivatives):
if derivatives == (1,):
return C_tang_impl
else:
raise NotImplementedError(f"No external function is defined for the requested derivative {derivatives}.")
sigma.external_function = sigma_external
Defining the forms#
q = fem.Constant(domain, default_scalar_type((0, -gamma)))
def F_ext(v):
return ufl.dot(q, v) * dx
u_hat = ufl.TrialFunction(V)
F = ufl.inner(epsilon(v), sigma) * dx - F_ext(v)
J = ufl.derivative(F, Du, u_hat)
J_expanded = ufl.algorithms.expand_derivatives(J)
F_replaced, F_external_operators = replace_external_operators(F)
J_replaced, J_external_operators = replace_external_operators(J_expanded)
F_form = fem.form(F_replaced)
J_form = fem.form(J_replaced)
Variables initialization and compilation#
Before solving the problem we have to initialize values of the stiffness matrix, as it requires for the system assembling. During the first loading step, we expect an elastic response only, so it’s enough to solve the constitutive equations for a relatively small displacement field at each Gauss point. This results in initializing the consistent tangent moduli with elastic ones.
Du.x.array[:] = 1.0
sigma_n.x.array[:] = 0.0
evaluated_operands = evaluate_operands(F_external_operators)
_ = evaluate_external_operators(J_external_operators, evaluated_operands)
Inner Newton summary:
Unique number of iterations: [1]
Counts of unique number of iterations: [3750]
Maximum f: -2.2109628558533108
Maximum residual: 0.0
Solving the problem#
Similarly to the von Mises tutorial, we use NonlinearProblem to solve the
global problem with SNES. To enable the external operators update at each
iteration of SNES before the vector and matrix assembly, we wrote a simple
wrapper assemble_residual_with_callback (see ./utilities.py)
petsc_options = {
"snes_type": "vinewtonrsls",
"snes_linesearch_type": "basic",
"ksp_type": "preonly",
"pc_type": "lu",
"pc_factor_mat_solver_type": "mumps",
"snes_atol": 1.0e-8,
"snes_rtol": 1.0e-8,
"snes_max_it": 100,
"snes_monitor": "",
}
problem = NonlinearProblem(
F_replaced, Du, J=J_replaced, bcs=bcs, petsc_options_prefix="demo_mohr-coulomb_", petsc_options=petsc_options
)
def constitutive_update():
evaluated_operands = evaluate_operands(F_external_operators)
((_, sigma_new),) = evaluate_external_operators(J_external_operators, evaluated_operands)
# Direct access to the external operator values
sigma.ref_coefficient.x.array[:] = sigma_new
assemble_residual_with_callback_ = partial(
assemble_residual_with_callback, problem.u, problem._F, problem._J, bcs, constitutive_update
)
problem.solver.setFunction(assemble_residual_with_callback_, problem.b)
After definition of the nonlinear problem and the Newton solver, we are ready to get the final result.
load_steps_1 = np.linspace(2, 22.9, 50)
load_steps_2 = np.array([22.96, 22.99])
load_steps = np.concatenate([load_steps_1, load_steps_2])
num_increments = len(load_steps)
results = np.zeros((num_increments + 1, 2))
x_point = np.array([[0, H, 0]])
cells, points_on_process = find_cell_by_point(domain, x_point)
for i, load in enumerate(load_steps):
q.value = load * np.array([0, -gamma])
if MPI.COMM_WORLD.rank == 0:
print(f"Load increment #{i}, load: {load}")
problem.solve()
u.x.petsc_vec.axpy(1.0, Du.x.petsc_vec)
u.x.scatter_forward()
sigma_n.x.array[:] = sigma.ref_coefficient.x.array
if len(points_on_process) > 0:
results[i + 1, :] = (-u.eval(points_on_process, cells)[0], load)
print(f"Slope stability factor: {-q.value[-1] * H / c}")
Load increment #0, load: 2.0
Inner Newton summary:
Unique number of iterations: [1]
Counts of unique number of iterations: [3750]
Maximum f: -2.2109628558533108
Maximum residual: 0.0
0 SNES Function norm 1.195147420875e+05
Inner Newton summary:
Unique number of iterations: [1]
Counts of unique number of iterations: [3750]
Maximum f: -0.754479661417915
Maximum residual: 0.0
1 SNES Function norm 4.904068111920e-10
Load increment #1, load: 2.426530612244898
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3748 2]
Maximum f: 1.1914324474182885
Maximum residual: 5.037137171928691e-10
0 SNES Function norm 4.756853160422e-02
Inner Newton summary:
Unique number of iterations: [1]
Counts of unique number of iterations: [3750]
Maximum f: -0.8092635980827123
Maximum residual: 2.3273757686693183e-16
1 SNES Function norm 3.033810662369e-02
Inner Newton summary:
Unique number of iterations: [1]
Counts of unique number of iterations: [3750]
Maximum f: -0.35079912068642827
Maximum residual: 2.498001805406602e-16
2 SNES Function norm 2.632871228115e-15
Load increment #2, load: 2.853061224489796
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3749 1]
Maximum f: 0.06115928116524261
Maximum residual: 1.625079471285139e-15
0 SNES Function norm 9.132432640845e-04
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3749 1]
Maximum f: 0.09230862184731725
Maximum residual: 8.863753529530979e-14
1 SNES Function norm 8.054297427641e-06
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3749 1]
Maximum f: 0.09244639358766138
Maximum residual: 9.003480198964377e-14
2 SNES Function norm 3.456153540816e-10
Load increment #3, load: 3.279591836734694
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3749 1]
Maximum f: 0.44844216521744684
Maximum residual: 1.1063094076276035e-13
0 SNES Function norm 5.392112070247e-03
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3748 2]
Maximum f: 0.6457397002297043
Maximum residual: 5.645165421208996e-09
1 SNES Function norm 9.222044508532e-04
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3748 2]
Maximum f: 0.6671698219110813
Maximum residual: 5.567802048440929e-09
2 SNES Function norm 2.306874770006e-06
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3748 2]
Maximum f: 0.6671780558585323
Maximum residual: 5.564613205182936e-09
3 SNES Function norm 8.267683443280e-12
Load increment #4, load: 3.706122448979592
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3748 2]
Maximum f: 0.6729159475629172
Maximum residual: 1.961913964273554e-09
0 SNES Function norm 7.708642137450e-03
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3748 2]
Maximum f: 0.8182731983589591
Maximum residual: 3.051809570897057e-09
1 SNES Function norm 1.306670391138e-04
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3748 2]
Maximum f: 0.8184517040414194
Maximum residual: 3.265751672265052e-09
2 SNES Function norm 1.677202587022e-08
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3748 2]
Maximum f: 0.8184520904141594
Maximum residual: 3.265798047927068e-09
3 SNES Function norm 2.674866273767e-15
Load increment #5, load: 4.13265306122449
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3747 3]
Maximum f: 0.8189820439289819
Maximum residual: 1.755743294289719e-09
0 SNES Function norm 6.653604188183e-03
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3747 3]
Maximum f: 0.9125840840028099
Maximum residual: 2.890914564407538e-09
1 SNES Function norm 2.564375080372e-05
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3747 3]
Maximum f: 0.9124710788798249
Maximum residual: 2.9132795603156254e-09
2 SNES Function norm 1.145551700990e-09
Load increment #6, load: 4.559183673469388
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3744 5 1]
Maximum f: 0.9120013616400873
Maximum residual: 2.0946149206421962e-09
0 SNES Function norm 4.373771847428e-03
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3744 5 1]
Maximum f: 1.083471686912659
Maximum residual: 7.0973714011107074e-09
1 SNES Function norm 9.084544888110e-05
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3744 5 1]
Maximum f: 1.0853634288842167
Maximum residual: 7.093968647337431e-09
2 SNES Function norm 1.607752517665e-08
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3744 5 1]
Maximum f: 1.0853639290780879
Maximum residual: 7.0939523452902265e-09
3 SNES Function norm 2.905322939888e-15
Load increment #7, load: 4.985714285714286
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3743 6 1]
Maximum f: 1.0817281941295964
Maximum residual: 6.9138245056056204e-09
0 SNES Function norm 7.149688794666e-03
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3743 5 2]
Maximum f: 1.3124494265785445
Maximum residual: 3.805485307832851e-09
1 SNES Function norm 2.058508967714e-04
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3743 5 2]
Maximum f: 1.3140149963446652
Maximum residual: 3.945091648573049e-09
2 SNES Function norm 7.527865371135e-08
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3743 5 2]
Maximum f: 1.3140158007718141
Maximum residual: 3.9451181841117385e-09
3 SNES Function norm 1.316313076856e-14
Load increment #8, load: 5.412244897959184
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3740 8 1 1]
Maximum f: 1.3088422717205206
Maximum residual: 7.66611460625318e-09
0 SNES Function norm 7.696175706972e-03
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3739 8 2 1]
Maximum f: 1.5216973741715996
Maximum residual: 1.4413461836633341e-08
1 SNES Function norm 5.990449202790e-04
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3739 7 3 1]
Maximum f: 1.5292334720682619
Maximum residual: 1.426873890872779e-08
2 SNES Function norm 4.936076056858e-07
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3739 7 3 1]
Maximum f: 1.5292375934479279
Maximum residual: 1.4268663442608312e-08
3 SNES Function norm 4.633444593166e-13
Load increment #9, load: 5.838775510204082
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3736 13 1]
Maximum f: 1.5243000402676876
Maximum residual: 7.68816236508426e-09
0 SNES Function norm 9.589791815981e-03
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3735 11 4]
Maximum f: 1.768982123620892
Maximum residual: 9.505123398506828e-09
1 SNES Function norm 3.862729558146e-04
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3735 11 4]
Maximum f: 1.7742284095842638
Maximum residual: 1.0807696717590483e-08
2 SNES Function norm 4.301313419683e-07
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3735 11 4]
Maximum f: 1.774233748804026
Maximum residual: 1.0809538722378203e-08
3 SNES Function norm 5.348012897413e-13
Load increment #10, load: 6.265306122448979
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3731 16 3]
Maximum f: 1.7693631620667758
Maximum residual: 1.059858585764075e-08
0 SNES Function norm 1.143203715428e-02
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3730 15 5]
Maximum f: 1.9314433466529155
Maximum residual: 1.4826213546618599e-08
1 SNES Function norm 1.584942427511e-03
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3730 14 6]
Maximum f: 1.9459812815294186
Maximum residual: 1.4853122531810609e-08
2 SNES Function norm 3.025107792004e-06
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3730 14 6]
Maximum f: 1.9460026016664025
Maximum residual: 1.4860223870507347e-08
3 SNES Function norm 1.580317603146e-11
Load increment #11, load: 6.691836734693877
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3724 22 2 2]
Maximum f: 1.9427232962954792
Maximum residual: 1.107082796918071e-08
0 SNES Function norm 1.107822857802e-02
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3723 18 6 3]
Maximum f: 2.122392164283412
Maximum residual: 1.7660578617363768e-08
1 SNES Function norm 5.672791184133e-04
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3723 18 6 3]
Maximum f: 2.127991178540578
Maximum residual: 1.804684480082454e-08
2 SNES Function norm 8.341174882008e-07
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3723 18 6 3]
Maximum f: 2.127999328205718
Maximum residual: 1.804726421460139e-08
3 SNES Function norm 1.851628693792e-12
Load increment #12, load: 7.118367346938775
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3719 27 4]
Maximum f: 2.125608307652828
Maximum residual: 1.2834182305331533e-08
0 SNES Function norm 1.211225124343e-02
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3716 24 9 1]
Maximum f: 2.3289082734777415
Maximum residual: 2.8296922459787262e-08
1 SNES Function norm 1.578810096150e-03
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3715 24 9 2]
Maximum f: 2.3415246200100612
Maximum residual: 1.829901438427389e-08
2 SNES Function norm 1.892066413846e-04
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3715 24 9 2]
Maximum f: 2.342448287388001
Maximum residual: 1.831880626766519e-08
3 SNES Function norm 3.305365333472e-08
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3715 24 9 2]
Maximum f: 2.3424484018720757
Maximum residual: 1.8318809329932305e-08
4 SNES Function norm 3.494392401265e-15
Load increment #13, load: 7.544897959183673
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3711 34 5]
Maximum f: 2.3401627518884447
Maximum residual: 2.5916483644494618e-08
0 SNES Function norm 1.196820342248e-02
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3710 28 12]
Maximum f: 2.5259332779377908
Maximum residual: 2.2868489990973495e-08
1 SNES Function norm 2.743993581195e-03
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3710 27 13]
Maximum f: 2.542296026957429
Maximum residual: 2.1308370407796376e-08
2 SNES Function norm 7.305829738902e-06
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3710 27 13]
Maximum f: 2.542333776222677
Maximum residual: 2.1310229723653986e-08
3 SNES Function norm 7.631494890250e-11
Load increment #14, load: 7.971428571428571
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3705 42 2 1]
Maximum f: 2.5402012017918953
Maximum residual: 1.429319323321139e-08
0 SNES Function norm 1.079588899770e-02
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3704 34 11 1]
Maximum f: 2.7285562243714154
Maximum residual: 2.287595921486507e-08
1 SNES Function norm 1.040283872579e-03
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3704 34 11 1]
Maximum f: 2.73630828486854
Maximum residual: 2.3842123866146033e-08
2 SNES Function norm 1.400314054705e-06
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3704 34 11 1]
Maximum f: 2.736317418830781
Maximum residual: 2.384323202254714e-08
3 SNES Function norm 2.772528240501e-12
Load increment #15, load: 8.397959183673468
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3699 49 2]
Maximum f: 2.734686952289232
Maximum residual: 7.159754441605131e-09
0 SNES Function norm 1.091345771982e-02
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3698 41 11]
Maximum f: 2.897365494402916
Maximum residual: 1.9947798457437588e-08
1 SNES Function norm 7.408397972280e-04
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3698 41 11]
Maximum f: 2.902394333239569
Maximum residual: 2.0634081750833236e-08
2 SNES Function norm 7.993577406882e-07
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3698 41 11]
Maximum f: 2.9023986347998227
Maximum residual: 2.0634616920893855e-08
3 SNES Function norm 8.010855224928e-13
Load increment #16, load: 8.824489795918367
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3693 1 54 2]
Maximum f: 2.901301302966727
Maximum residual: 7.082321828410761e-09
0 SNES Function norm 1.131724631643e-02
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3692 53 5]
Maximum f: 3.0562073612070635
Maximum residual: 1.9590593259503147e-08
1 SNES Function norm 1.008710940736e-03
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3692 51 7]
Maximum f: 3.0611886840094082
Maximum residual: 2.0280904881026746e-08
2 SNES Function norm 1.574785763049e-06
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3692 51 7]
Maximum f: 3.0611926039834274
Maximum residual: 2.028144679170965e-08
3 SNES Function norm 3.672581922296e-12
Load increment #17, load: 9.251020408163264
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3688 61 1]
Maximum f: 3.0606359799273943
Maximum residual: 4.539286410264927e-09
0 SNES Function norm 1.039626377063e-02
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3687 57 6]
Maximum f: 3.1932576381580096
Maximum residual: 1.3834417330573261e-08
1 SNES Function norm 5.727495097146e-04
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3687 57 6]
Maximum f: 3.196406185774563
Maximum residual: 1.4192616341080524e-08
2 SNES Function norm 4.430536444174e-07
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3687 57 6]
Maximum f: 3.1964077098125494
Maximum residual: 1.4192788631431939e-08
3 SNES Function norm 2.390106606130e-13
Load increment #18, load: 9.677551020408163
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3682 67 1]
Maximum f: 3.196279234543097
Maximum residual: 3.128096602809281e-09
0 SNES Function norm 1.077705186543e-02
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3682 63 5]
Maximum f: 3.3273846790635466
Maximum residual: 3.006978540899422e-08
1 SNES Function norm 2.242198150757e-04
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3682 63 5]
Maximum f: 3.3291427526630843
Maximum residual: 3.1822786253566305e-08
2 SNES Function norm 8.066505839047e-08
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3682 63 5]
Maximum f: 3.329143179517779
Maximum residual: 3.182323775492317e-08
3 SNES Function norm 1.183930747079e-14
Load increment #19, load: 10.10408163265306
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3677 3 68 1 1]
Maximum f: 3.3293810538315536
Maximum residual: 2.401541510930868e-08
0 SNES Function norm 1.009301544127e-02
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3676 69 4 1]
Maximum f: 3.4464888773195432
Maximum residual: 2.190374447323829e-08
1 SNES Function norm 2.451203768063e-04
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3676 69 4 1]
Maximum f: 3.447255273164005
Maximum residual: 1.8753968735879454e-08
2 SNES Function norm 6.772470639976e-08
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3676 69 4 1]
Maximum f: 3.44725581778417
Maximum residual: 1.8754300554902312e-08
3 SNES Function norm 1.178080770902e-14
Load increment #20, load: 10.530612244897958
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3673 75 2]
Maximum f: 3.4477457741927204
Maximum residual: 1.230092407528599e-08
0 SNES Function norm 8.769338038872e-03
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3672 74 4]
Maximum f: 3.5536122340135248
Maximum residual: 2.0731769519867258e-08
1 SNES Function norm 1.398871589577e-03
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3672 74 4]
Maximum f: 3.5575500941879716
Maximum residual: 2.08800105514932e-08
2 SNES Function norm 1.379070835962e-06
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3672 74 4]
Maximum f: 3.557553374057784
Maximum residual: 2.0880045160635553e-08
3 SNES Function norm 2.265891313229e-12
Load increment #21, load: 10.957142857142856
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3669 79 2]
Maximum f: 3.5582224238556868
Maximum residual: 1.3134271979621058e-09
0 SNES Function norm 8.691186079801e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3669 2 75 4]
Maximum f: 3.657593942592117
Maximum residual: 3.5954579661102315e-08
1 SNES Function norm 3.411985921926e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3669 1 76 4]
Maximum f: 3.660080990277345
Maximum residual: 2.9021563003902195e-09
2 SNES Function norm 2.666288752882e-06
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3669 1 76 4]
Maximum f: 3.660081030314147
Maximum residual: 2.9021525172151927e-09
3 SNES Function norm 1.419469593806e-11
Load increment #22, load: 11.383673469387753
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3664 3 82 1]
Maximum f: 3.6608897267290836
Maximum residual: 2.6397934919251335e-08
0 SNES Function norm 8.784785795509e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3662 2 84 2]
Maximum f: 3.751648638769233
Maximum residual: 4.6779431156866174e-08
1 SNES Function norm 2.334921659320e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3662 1 85 2]
Maximum f: 3.7550666405164423
Maximum residual: 4.7243835173141243e-08
2 SNES Function norm 9.229833616511e-06
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3662 1 85 2]
Maximum f: 3.755069894493355
Maximum residual: 4.724239079614478e-08
3 SNES Function norm 1.329652467664e-10
Load increment #23, load: 11.810204081632651
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3660 4 84 2]
Maximum f: 3.7559609444110253
Maximum residual: 3.3906255731840494e-08
0 SNES Function norm 7.703871014509e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3659 3 85 3]
Maximum f: 3.8382982030471386
Maximum residual: 2.1412607277191686e-08
1 SNES Function norm 7.732693973154e-04
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3659 2 86 3]
Maximum f: 3.839826825119902
Maximum residual: 2.18161139671377e-08
2 SNES Function norm 4.461456405324e-06
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3659 2 86 3]
Maximum f: 3.839829098626676
Maximum residual: 2.1815659912685375e-08
3 SNES Function norm 6.876425366237e-11
Load increment #24, load: 12.23673469387755
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3653 3 91 3]
Maximum f: 3.8407568214012815
Maximum residual: 4.205786735675998e-08
0 SNES Function norm 1.146900093023e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3652 1 94 3]
Maximum f: 3.9276871850441
Maximum residual: 5.796850285049134e-08
1 SNES Function norm 2.495998296202e-03
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3653 94 3]
Maximum f: 3.931199398279342
Maximum residual: 5.724728568625639e-08
2 SNES Function norm 1.623104017190e-05
Inner Newton summary:
Unique number of iterations: [1 3 4]
Counts of unique number of iterations: [3653 94 3]
Maximum f: 3.931205210614485
Maximum residual: 5.724501937531905e-08
3 SNES Function norm 3.768453775931e-10
Load increment #25, load: 12.663265306122447
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3644 4 99 2 1]
Maximum f: 3.9321439660188813
Maximum residual: 5.062351656908394e-09
0 SNES Function norm 8.353184330108e-03
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3646 101 2 1]
Maximum f: 4.327729961142188
Maximum residual: 3.233388817228885e-08
1 SNES Function norm 8.334150687845e-03
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3646 101 2 1]
Maximum f: 4.311288264135275
Maximum residual: 3.239739744902397e-08
2 SNES Function norm 4.637932353034e-06
Inner Newton summary:
Unique number of iterations: [1 3 4 5]
Counts of unique number of iterations: [3646 101 2 1]
Maximum f: 4.311303131281337
Maximum residual: 3.2397028532239655e-08
3 SNES Function norm 2.609545489094e-11
Load increment #26, load: 13.089795918367345
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3639 1 108 2]
Maximum f: 4.313176238016512
Maximum residual: 2.9576099199710677e-08
0 SNES Function norm 1.194001516472e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3637 2 108 3]
Maximum f: 4.8672539288163
Maximum residual: 1.7686694834542354e-08
1 SNES Function norm 6.098877544132e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3638 2 107 3]
Maximum f: 4.959680353880238
Maximum residual: 1.6621644591881908e-08
2 SNES Function norm 1.108269377349e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3638 2 107 3]
Maximum f: 4.956079107449442
Maximum residual: 1.6609212763592716e-08
3 SNES Function norm 3.073549375006e-07
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3638 2 107 3]
Maximum f: 4.956077715188007
Maximum residual: 1.6609210024779162e-08
4 SNES Function norm 1.136640149044e-13
Load increment #27, load: 13.516326530612243
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3628 5 116 1]
Maximum f: 4.957344021789531
Maximum residual: 1.811708041153886e-08
0 SNES Function norm 1.240366718545e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3628 3 116 3]
Maximum f: 5.683701149471101
Maximum residual: 1.2958279001161183e-08
1 SNES Function norm 2.161926288287e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3627 4 115 4]
Maximum f: 5.720335933291569
Maximum residual: 1.2955191874983027e-08
2 SNES Function norm 1.004507493488e-04
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3627 4 115 4]
Maximum f: 5.722494932268287
Maximum residual: 1.2857682707418678e-08
3 SNES Function norm 3.137931197027e-08
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3627 4 115 4]
Maximum f: 5.722495071385577
Maximum residual: 1.2857664855822849e-08
4 SNES Function norm 4.687028855665e-15
Load increment #28, load: 13.942857142857141
Inner Newton summary:
Unique number of iterations: [1 2 3]
Counts of unique number of iterations: [3620 3 127]
Maximum f: 5.7235713109107405
Maximum residual: 8.619153711760841e-09
0 SNES Function norm 1.195591532823e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3616 2 129 3]
Maximum f: 6.645080068812925
Maximum residual: 1.7387325035989483e-08
1 SNES Function norm 4.874621421367e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3616 1 130 3]
Maximum f: 6.811772121665655
Maximum residual: 1.892052728057244e-08
2 SNES Function norm 6.244285417529e-05
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3616 1 130 3]
Maximum f: 6.812691928883799
Maximum residual: 1.8927762138736194e-08
3 SNES Function norm 8.457653534142e-09
Load increment #29, load: 14.36938775510204
Inner Newton summary:
Unique number of iterations: [1 2 3]
Counts of unique number of iterations: [3608 4 138]
Maximum f: 6.813577582394872
Maximum residual: 2.6390513232677924e-08
0 SNES Function norm 1.319402690197e-02
Inner Newton summary:
Unique number of iterations: [1 2 3]
Counts of unique number of iterations: [3607 2 141]
Maximum f: 7.596225865539276
Maximum residual: 2.7316572655506915e-08
1 SNES Function norm 6.000358681717e-03
Inner Newton summary:
Unique number of iterations: [1 2 3]
Counts of unique number of iterations: [3607 2 141]
Maximum f: 7.662614238371008
Maximum residual: 3.175527862366224e-08
2 SNES Function norm 2.231686172704e-05
Inner Newton summary:
Unique number of iterations: [1 2 3]
Counts of unique number of iterations: [3607 2 141]
Maximum f: 7.66266956245464
Maximum residual: 3.176597448193741e-08
3 SNES Function norm 8.253913866558e-10
Load increment #30, load: 14.795918367346937
Inner Newton summary:
Unique number of iterations: [1 2 3]
Counts of unique number of iterations: [3595 6 149]
Maximum f: 7.663139576851158
Maximum residual: 2.236738313473024e-08
0 SNES Function norm 1.503558807032e-02
Inner Newton summary:
Unique number of iterations: [1 2 3]
Counts of unique number of iterations: [3594 3 153]
Maximum f: 8.454917434393005
Maximum residual: 2.0862189585625437e-08
1 SNES Function norm 6.182460517857e-03
Inner Newton summary:
Unique number of iterations: [1 2 3]
Counts of unique number of iterations: [3594 3 153]
Maximum f: 8.561832222793015
Maximum residual: 2.611771224831483e-08
2 SNES Function norm 5.709638472826e-05
Inner Newton summary:
Unique number of iterations: [1 2 3]
Counts of unique number of iterations: [3594 3 153]
Maximum f: 8.562225052308744
Maximum residual: 2.6136947459011337e-08
3 SNES Function norm 6.605695834019e-09
Load increment #31, load: 15.222448979591835
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3582 6 161 1]
Maximum f: 8.562438155256226
Maximum residual: 5.366137756569831e-08
0 SNES Function norm 1.356272783579e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3578 7 162 2 1]
Maximum f: 9.462706125067632
Maximum residual: 2.9615100134770945e-08
1 SNES Function norm 1.108959098908e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3578 6 163 2 1]
Maximum f: 9.531525798162777
Maximum residual: 3.642435033332106e-08
2 SNES Function norm 2.776717567059e-05
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3578 6 163 2 1]
Maximum f: 9.531403525835428
Maximum residual: 3.66726451377794e-08
3 SNES Function norm 1.547137244295e-09
Load increment #32, load: 15.648979591836733
Inner Newton summary:
Unique number of iterations: [1 2 3 5]
Counts of unique number of iterations: [3558 6 185 1]
Maximum f: 9.5315076636003
Maximum residual: 2.2943693825458262e-08
0 SNES Function norm 1.690023171389e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3555 2 188 4 1]
Maximum f: 11.208475801671021
Maximum residual: 1.392556860469605e-08
1 SNES Function norm 1.136486356816e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3555 1 189 4 1]
Maximum f: 11.328808304184696
Maximum residual: 2.071183419683419e-08
2 SNES Function norm 4.043685669757e-05
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3555 1 189 4 1]
Maximum f: 11.328996289219972
Maximum residual: 2.073873611282863e-08
3 SNES Function norm 3.107153926162e-09
Load increment #33, load: 16.07551020408163
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3542 2 204 2]
Maximum f: 11.329238008815352
Maximum residual: 1.1473379486336675e-08
0 SNES Function norm 1.445355802854e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3540 4 198 8]
Maximum f: 12.390016864905776
Maximum residual: 3.4816166600395587e-08
1 SNES Function norm 8.639360130456e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3540 6 196 8]
Maximum f: 12.473904687662142
Maximum residual: 5.455887294248041e-08
2 SNES Function norm 1.258589840391e-05
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3540 6 196 8]
Maximum f: 12.473963542525862
Maximum residual: 5.447863970491717e-08
3 SNES Function norm 2.119207571829e-10
Load increment #34, load: 16.502040816326527
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3522 7 219 2]
Maximum f: 12.474040223165616
Maximum residual: 3.0852741220911174e-08
0 SNES Function norm 1.409596865654e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3522 10 210 8]
Maximum f: 13.621030460090084
Maximum residual: 2.683815052962345e-08
1 SNES Function norm 3.751124853547e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3520 10 212 8]
Maximum f: 13.672897613109884
Maximum residual: 3.524290551209748e-08
2 SNES Function norm 1.294558689652e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3521 9 212 8]
Maximum f: 13.683042197974578
Maximum residual: 3.0360430387253114e-08
3 SNES Function norm 5.415828097364e-05
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3521 9 212 8]
Maximum f: 13.683257893898473
Maximum residual: 3.0314245300185444e-08
4 SNES Function norm 1.090266585173e-09
Load increment #35, load: 16.928571428571427
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3507 13 229 1]
Maximum f: 13.683249738187508
Maximum residual: 1.8274117125821625e-08
0 SNES Function norm 1.773988907407e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3499 4 238 9]
Maximum f: 15.181050137106014
Maximum residual: 5.3359730715763754e-08
1 SNES Function norm 4.041295762343e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3499 4 238 9]
Maximum f: 15.29368739099492
Maximum residual: 2.382814809002762e-08
2 SNES Function norm 2.084752657082e-05
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3499 4 238 9]
Maximum f: 15.29364120617227
Maximum residual: 2.383595802751946e-08
3 SNES Function norm 5.396666841072e-10
Load increment #36, load: 17.355102040816327
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3480 11 258 1]
Maximum f: 15.293621570476697
Maximum residual: 4.3733266247192296e-08
0 SNES Function norm 1.733879266120e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3478 7 254 11]
Maximum f: 16.65829634458386
Maximum residual: 4.011337120327239e-08
1 SNES Function norm 1.499749094517e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3478 5 256 11]
Maximum f: 16.753380479727234
Maximum residual: 1.198683180194611e-08
2 SNES Function norm 3.007459439810e-05
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3478 5 256 11]
Maximum f: 16.75373917785474
Maximum residual: 1.1976573625733263e-08
3 SNES Function norm 1.425970985738e-09
Load increment #37, load: 17.781632653061223
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3464 11 273 1 1]
Maximum f: 16.753695524790697
Maximum residual: 5.451325695873651e-08
0 SNES Function norm 1.861829821566e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3461 11 271 5 2]
Maximum f: 18.047630053481384
Maximum residual: 6.10041136289682e-08
1 SNES Function norm 2.630504081379e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3460 8 275 5 2]
Maximum f: 18.1094396987448
Maximum residual: 7.997604018604162e-08
2 SNES Function norm 3.124568213974e-05
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3460 8 275 5 2]
Maximum f: 18.109954270130682
Maximum residual: 8.03206426332449e-08
3 SNES Function norm 2.300727907668e-09
Load increment #38, load: 18.20816326530612
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3435 8 305 2]
Maximum f: 18.1098668947868
Maximum residual: 3.543844458565271e-08
0 SNES Function norm 1.800669384053e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3427 8 309 6]
Maximum f: 19.68263641752709
Maximum residual: 5.462722577926099e-08
1 SNES Function norm 4.274620709122e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3427 7 310 6]
Maximum f: 19.816059584913543
Maximum residual: 7.360482400325298e-08
2 SNES Function norm 2.487642596236e-05
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3427 7 310 6]
Maximum f: 19.816699769298644
Maximum residual: 7.313229529811144e-08
3 SNES Function norm 1.096984719826e-09
Load increment #39, load: 18.63469387755102
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3407 15 325 3]
Maximum f: 19.81660860338259
Maximum residual: 3.29477267792261e-08
0 SNES Function norm 1.931304808040e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3406 7 328 9]
Maximum f: 21.389004861044686
Maximum residual: 4.958933134707706e-08
1 SNES Function norm 5.092741146638e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3406 7 328 9]
Maximum f: 21.480123702404175
Maximum residual: 5.538557966677485e-08
2 SNES Function norm 2.203884275238e-05
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3406 7 328 9]
Maximum f: 21.48012817615866
Maximum residual: 5.53953675602519e-08
3 SNES Function norm 1.122075514103e-09
Load increment #40, load: 19.061224489795915
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3385 13 350 2]
Maximum f: 21.480018052307305
Maximum residual: 3.93505517677384e-08
0 SNES Function norm 1.807185057934e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3377 14 351 8]
Maximum f: 23.101864004082827
Maximum residual: 7.48932527700298e-08
1 SNES Function norm 4.096957992682e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3376 8 358 8]
Maximum f: 23.181233427975545
Maximum residual: 5.4376244356055e-08
2 SNES Function norm 3.801885713099e-04
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3376 7 359 8]
Maximum f: 23.185942545326444
Maximum residual: 5.475291283959161e-08
3 SNES Function norm 2.086410192134e-08
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3376 7 359 8]
Maximum f: 23.18594259385966
Maximum residual: 5.47529050543232e-08
4 SNES Function norm 6.542633376631e-15
Load increment #41, load: 19.487755102040815
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3356 11 381 2]
Maximum f: 23.185822012668407
Maximum residual: 6.081587897387662e-08
0 SNES Function norm 2.318768587420e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3352 6 380 11 1]
Maximum f: 25.497168088941965
Maximum residual: 4.983963872735488e-08
1 SNES Function norm 5.854691572877e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3351 6 382 10 1]
Maximum f: 25.567903421737167
Maximum residual: 7.710589432980409e-08
2 SNES Function norm 1.857969440167e-04
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3351 6 382 10 1]
Maximum f: 25.570064621334264
Maximum residual: 7.630891480071638e-08
3 SNES Function norm 1.324273257589e-07
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3351 6 382 10 1]
Maximum f: 25.570065383153505
Maximum residual: 7.63088244829472e-08
4 SNES Function norm 4.516812210932e-14
Load increment #42, load: 19.91428571428571
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3324 11 413 1 1]
Maximum f: 25.56996105387755
Maximum residual: 5.6060587792713385e-08
0 SNES Function norm 1.991950861898e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3320 6 413 10 1]
Maximum f: 27.48539921969236
Maximum residual: 4.017158764340321e-08
1 SNES Function norm 6.102183392930e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3320 8 411 10 1]
Maximum f: 27.60556017048542
Maximum residual: 3.686313959913582e-08
2 SNES Function norm 5.558752205575e-05
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3320 8 411 10 1]
Maximum f: 27.60571575729927
Maximum residual: 3.684919745999727e-08
3 SNES Function norm 7.661646675665e-09
Load increment #43, load: 20.34081632653061
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3291 14 444 1]
Maximum f: 27.60558602282006
Maximum residual: 5.775546416597602e-08
0 SNES Function norm 2.099035542902e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3288 11 443 8]
Maximum f: 29.843867326127075
Maximum residual: 7.13978195271883e-08
1 SNES Function norm 4.733736371878e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3289 11 442 8]
Maximum f: 29.969805340763983
Maximum residual: 6.912247567673602e-08
2 SNES Function norm 5.313476427747e-04
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3289 11 442 8]
Maximum f: 29.97403243340984
Maximum residual: 6.694396573908324e-08
3 SNES Function norm 1.094543343557e-07
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3289 11 442 8]
Maximum f: 29.97403261643209
Maximum residual: 6.694298719752623e-08
4 SNES Function norm 1.334799882724e-14
Load increment #44, load: 20.767346938775507
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3259 20 469 2]
Maximum f: 29.973884886574034
Maximum residual: 6.014568573930785e-08
0 SNES Function norm 2.246453731859e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3253 15 472 10]
Maximum f: 32.90205667394853
Maximum residual: 4.978738638774052e-08
1 SNES Function norm 4.783821924576e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3254 9 477 10]
Maximum f: 33.077034350092866
Maximum residual: 5.3298265875618106e-08
2 SNES Function norm 5.291518412056e-04
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3254 9 477 10]
Maximum f: 33.08102796048972
Maximum residual: 5.3375795250022777e-08
3 SNES Function norm 4.903824828321e-08
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3254 9 477 10]
Maximum f: 33.08102797676846
Maximum residual: 5.33757992672904e-08
4 SNES Function norm 8.152375128904e-15
Load increment #45, load: 21.193877551020407
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3222 14 512 1 1]
Maximum f: 33.080883036235605
Maximum residual: 4.5861973161415454e-08
0 SNES Function norm 2.150367183099e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3214 14 509 12 1]
Maximum f: 36.42903952633922
Maximum residual: 6.060363095946784e-08
1 SNES Function norm 8.415327791299e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3212 14 512 11 1]
Maximum f: 36.59087082197456
Maximum residual: 7.033600568184792e-08
2 SNES Function norm 2.624314374599e-04
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3212 14 512 11 1]
Maximum f: 36.5928392616246
Maximum residual: 7.04186713412719e-08
3 SNES Function norm 2.176387423161e-07
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3212 14 512 11 1]
Maximum f: 36.592840384997906
Maximum residual: 7.041868428415607e-08
4 SNES Function norm 1.348641728657e-13
Load increment #46, load: 21.620408163265303
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3178 21 549 1 1]
Maximum f: 36.592683957433856
Maximum residual: 2.3037648358093993e-08
0 SNES Function norm 2.628890154187e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3175 15 548 12]
Maximum f: 40.88016399782628
Maximum residual: 4.861052053819875e-08
1 SNES Function norm 9.704135791354e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3174 13 551 12]
Maximum f: 41.0968804458801
Maximum residual: 5.888597366794194e-08
2 SNES Function norm 3.940138059941e-04
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3174 13 551 12]
Maximum f: 41.09933447019438
Maximum residual: 5.8958584316707404e-08
3 SNES Function norm 3.404476110840e-07
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3174 13 551 12]
Maximum f: 41.09933731996515
Maximum residual: 5.895863909888041e-08
4 SNES Function norm 3.269968745409e-13
Load increment #47, load: 22.046938775510203
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3138 21 588 3]
Maximum f: 41.099162405545904
Maximum residual: 1.5081275470153627e-07
0 SNES Function norm 2.587384322553e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3129 27 582 12]
Maximum f: 46.39966838688691
Maximum residual: 6.262153314782439e-08
1 SNES Function norm 6.838178297473e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3127 21 589 12 1]
Maximum f: 46.93592390989388
Maximum residual: 1.0299805581185181e-07
2 SNES Function norm 1.362075338948e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3127 19 591 12 1]
Maximum f: 46.97212287391886
Maximum residual: 8.753638439448589e-08
3 SNES Function norm 8.572437203118e-06
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3127 19 591 12 1]
Maximum f: 46.97221015126655
Maximum residual: 8.753995697853493e-08
4 SNES Function norm 1.261713276493e-10
Load increment #48, load: 22.4734693877551
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3086 30 627 7]
Maximum f: 46.972031392274054
Maximum residual: 6.743331251673834e-08
0 SNES Function norm 2.944549916639e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3072 26 633 19]
Maximum f: 54.79142280645256
Maximum residual: 1.280752704048728e-07
1 SNES Function norm 1.035617501699e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3072 25 634 19]
Maximum f: 55.92681732819214
Maximum residual: 1.944303862200015e-07
2 SNES Function norm 1.664047906161e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3072 23 637 18]
Maximum f: 55.971270307492325
Maximum residual: 1.9966759483910876e-07
3 SNES Function norm 6.382437508192e-06
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [3072 23 637 18]
Maximum f: 55.97133470774837
Maximum residual: 1.9967645082915702e-07
4 SNES Function norm 1.046911016687e-10
Load increment #49, load: 22.9
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [3006 36 697 10 1]
Maximum f: 55.97111640595403
Maximum residual: 9.181422240836748e-08
0 SNES Function norm 3.451445654693e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [2979 20 730 20 1]
Maximum f: 71.24902596407976
Maximum residual: 1.7736360683341544e-07
1 SNES Function norm 3.791796477487e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [2971 20 726 32 1]
Maximum f: 78.51083340525066
Maximum residual: 3.4224984788998346e-07
2 SNES Function norm 6.547900362150e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [2973 18 725 33 1]
Maximum f: 79.67788407053465
Maximum residual: 5.530155025625651e-07
3 SNES Function norm 1.411257682784e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [2973 18 725 33 1]
Maximum f: 79.7736403579505
Maximum residual: 5.717286876920083e-07
4 SNES Function norm 1.114569889285e-04
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [2973 18 725 33 1]
Maximum f: 79.77518101584522
Maximum residual: 5.719374214226168e-07
5 SNES Function norm 1.307185572722e-08
Inner Newton summary:
Unique number of iterations: [1 2 3 4 5]
Counts of unique number of iterations: [2973 18 725 33 1]
Maximum f: 79.77518100703828
Maximum residual: 5.719374244420973e-07
6 SNES Function norm 1.493443155002e-14
Load increment #50, load: 22.96
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [2875 27 823 25]
Maximum f: 79.77483948791324
Maximum residual: 7.72099747489702e-08
0 SNES Function norm 4.510532966358e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [2980 163 590 17]
Maximum f: 18.04068353681255
Maximum residual: 3.2623013182061e-08
1 SNES Function norm 3.813905199852e-01
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [2956 143 646 5]
Maximum f: 21.19212798427213
Maximum residual: 3.2211716435755484e-08
2 SNES Function norm 2.731881915507e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [2939 126 676 9]
Maximum f: 27.35877462534555
Maximum residual: 3.970759477156723e-08
3 SNES Function norm 9.518819283937e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [2937 103 700 10]
Maximum f: 32.93695984913357
Maximum residual: 7.979459135231512e-08
4 SNES Function norm 2.440368481890e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [2935 101 703 11]
Maximum f: 34.048736088512456
Maximum residual: 2.4912422790275553e-08
5 SNES Function norm 4.704398167595e-04
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [2935 101 703 11]
Maximum f: 34.14222362720707
Maximum residual: 2.4406671435981175e-08
6 SNES Function norm 1.117573930042e-06
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [2935 101 703 11]
Maximum f: 34.14235387239332
Maximum residual: 2.4406105498607996e-08
7 SNES Function norm 5.486597357809e-12
Load increment #51, load: 22.99
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [2923 112 712 3]
Maximum f: 34.14219556832736
Maximum residual: 6.430010633117862e-08
0 SNES Function norm 1.458357152583e-02
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [2925 161 662 2]
Maximum f: 29.880260321827002
Maximum residual: 2.927566778126675e-08
1 SNES Function norm 5.932855542944e-03
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [2926 157 665 2]
Maximum f: 31.32107837332203
Maximum residual: 3.33433776919066e-08
2 SNES Function norm 6.233209758949e-04
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [2926 157 665 2]
Maximum f: 31.363803938674593
Maximum residual: 3.320235811489407e-08
3 SNES Function norm 4.410931140174e-07
Inner Newton summary:
Unique number of iterations: [1 2 3 4]
Counts of unique number of iterations: [2926 157 665 2]
Maximum f: 31.363876920814384
Maximum residual: 3.3202640922767024e-08
4 SNES Function norm 1.805174821103e-12
Slope stability factor: 6.663768115942029
Verification#
Critical load#
According to Chen and Liu [1990], we can derive analytically the slope stability factor \(l_\text{lim}\) for the standard Mohr-Coulomb plasticity model (without apex smoothing) under plane strain assumption for associative plastic flow
\[
l_\text{lim} = \gamma_\text{lim} H/c,
\]
where \(\gamma_\text{lim}\) is an associated value of the soil self-weight. In particular, for the rectangular slope with the friction angle \(\phi\) equal to \(30^\circ\), \(l_\text{lim} = 6.69\) [Chen and Liu, 1990]. Thus, by computing \(\gamma_\text{lim}\) from the formula above, we can progressively increase the second component of the gravitational body force \(\boldsymbol{q}=[0, -\gamma]^T\), up to the critical value \(\gamma_\text{lim}^\text{num}\), when the perfect plasticity plateau is reached on the loading-displacement curve at the \((0, H)\) point and then compare \(\gamma_\text{lim}^\text{num}\) against analytical \(\gamma_\text{lim}\).
By demonstrating the loading-displacement curve on the figure below we approve that the yield strength limit reached for \(\gamma_\text{lim}^\text{num}\) is close to \(\gamma_\text{lim}\).
if len(points_on_process) > 0:
l_lim = 6.69
gamma_lim = l_lim / H * c
plt.plot(results[:, 0], results[:, 1], "o-", label=r"$\gamma$")
plt.axhline(y=gamma_lim, color="r", linestyle="--", label=r"$\gamma_\text{lim}$")
plt.xlabel(r"Displacement of the slope $u_x$ at $(0, H)$ [mm]")
plt.ylabel(r"Soil self-weight $\gamma$ [MPa/mm$^3$]")
plt.grid()
plt.legend()
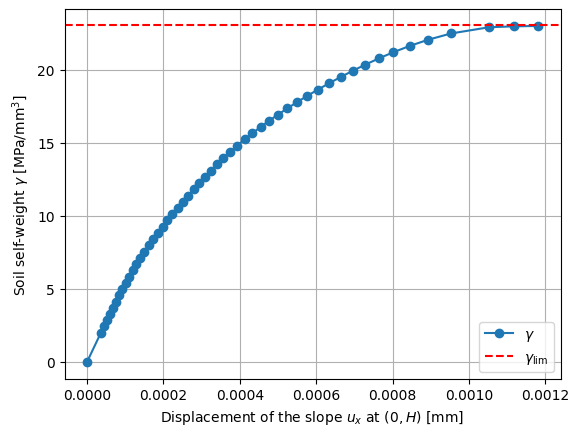
The slope profile reaching its stability limit:
try:
import pyvista
print(pyvista.global_theme.jupyter_backend)
import dolfinx.plot
W = fem.functionspace(domain, ("Lagrange", 1, (gdim,)))
u_tmp = fem.Function(W, name="Displacement")
u_tmp.interpolate(u)
plotter = pyvista.Plotter(window_size=[600, 400], off_screen=True)
topology, cell_types, x = dolfinx.plot.vtk_mesh(domain)
grid = pyvista.UnstructuredGrid(topology, cell_types, x)
vals = np.zeros((x.shape[0], 3))
vals[:, : len(u_tmp)] = u_tmp.x.array.reshape((x.shape[0], len(u_tmp)))
grid["u"] = vals
warped = grid.warp_by_vector("u", factor=20)
plotter.add_mesh(warped, show_edges=False, show_scalar_bar=False)
plotter.view_xy()
plotter.camera.tight()
image = plotter.screenshot(None, transparent_background=True, return_img=True)
plt.imshow(image)
plt.axis("off")
except ImportError:
print("pyvista required for this plot")
static
2025-10-24 13:59:02.115 ( 0.494s) [ 7F61FBE67140]vtkXOpenGLRenderWindow.:1458 WARN| bad X server connection. DISPLAY=:99.0
Yield surface#
We verify that the constitutive model is correctly implemented by tracing the yield surface. We generate several stress paths and check whether they remain within the Mohr-Coulomb yield surface. The stress tracing is performed in the Haigh-Westergaard coordinates \((\xi, \rho, \theta)\) which are defined as follows
\[
\xi = \frac{1}{\sqrt{3}}I_1, \quad \rho =
\sqrt{2J_2}, \quad \sin(3\theta) = -\frac{3\sqrt{3}}{2}
\frac{J_3}{J_2^{3/2}},
\]
where \(J_3(\boldsymbol{\sigma}) = \det(\boldsymbol{s})\) is the third invariant of the deviatoric part of the stress tensor, \(\xi\) is the deviatoric coordinate, \(\rho\) is the radial coordinate and the angle \(\theta \in [-\frac{\pi}{6}, \frac{\pi}{6}]\) is called Lode or stress angle.
To generate the stress paths we use the principal stresses formula written in Haigh-Westergaard coordinates as follows
\[\begin{split}
\begin{pmatrix}
\sigma_{I} \\
\sigma_{II} \\
\sigma_{III}
\end{pmatrix}
= p
\begin{pmatrix}
1 \\
1 \\
1
\end{pmatrix}
+ \frac{\rho}{\sqrt{2}}
\begin{pmatrix}
\cos\theta + \frac{\sin\theta}{\sqrt{3}} \\
-\frac{2\sin\theta}{\sqrt{3}} \\
\frac{\sin\theta}{\sqrt{3}} - \cos\theta
\end{pmatrix},
\end{split}\]
where \(p = \xi/\sqrt{3}\) is a hydrostatic variable and \(\sigma_{I} \geq \sigma_{II} \geq \sigma_{III}\).
Now we generate the loading path by evaluating principal stresses in Haigh-Westergaard coordinates for the Lode angle \(\theta\) being varied from \(-\frac{\pi}{6}\) to \(\frac{\pi}{6}\) with fixed \(\rho\) and \(p\).
N_angles = 50
N_loads = 9 # number of loadings or paths
eps = 0.00001
R = 0.7 # fix the values of rho
p = 0.1 # fix the deviatoric coordinate
theta_1 = -np.pi / 6
theta_2 = np.pi / 6
theta_values = np.linspace(theta_1 + eps, theta_2 - eps, N_angles)
theta_returned = np.empty((N_loads, N_angles))
rho_returned = np.empty((N_loads, N_angles))
sigma_returned = np.empty((N_loads, N_angles, stress_dim))
# fix an increment of the stress path
dsigma_path = np.zeros((N_angles, stress_dim))
dsigma_path[:, 0] = (R / np.sqrt(2)) * (np.cos(theta_values) + np.sin(theta_values) / np.sqrt(3))
dsigma_path[:, 1] = (R / np.sqrt(2)) * (-2 * np.sin(theta_values) / np.sqrt(3))
dsigma_path[:, 2] = (R / np.sqrt(2)) * (np.sin(theta_values) / np.sqrt(3) - np.cos(theta_values))
sigma_n_local = np.zeros_like(dsigma_path)
sigma_n_local[:, 0] = p
sigma_n_local[:, 1] = p
sigma_n_local[:, 2] = p
derviatoric_axis = tr
Then, we define and vectorize functions rho, Lode_angle and sigma_tracing
evaluating respectively the coordinates \(\rho\), \(\theta\) and the corrected (or
“returned”) stress tensor for a certain stress state. sigma_tracing calls the
function return_mapping, where the constitutive model was defined via JAX
previously.
def rho(sigma_local):
s = dev @ sigma_local
return jnp.sqrt(2.0 * J2(s))
def Lode_angle(sigma_local):
s = dev @ sigma_local
arg = -(3.0 * jnp.sqrt(3.0) * J3(s)) / (2.0 * jnp.sqrt(J2(s) * J2(s) * J2(s)))
arg = jnp.clip(arg, -1.0, 1.0)
angle = 1.0 / 3.0 * jnp.arcsin(arg)
return angle
def sigma_tracing(sigma_local, sigma_n_local):
deps_elas = S_elas @ sigma_local
sigma_corrected, state = return_mapping(deps_elas, sigma_n_local)
yielding = state[2]
return sigma_corrected, yielding
Lode_angle_v = jax.jit(jax.vmap(Lode_angle, in_axes=(0)))
rho_v = jax.jit(jax.vmap(rho, in_axes=(0)))
sigma_tracing_v = jax.jit(jax.vmap(sigma_tracing, in_axes=(0, 0)))
For each stress path, we call the function sigma_tracing_v to get the
corrected stress state and then we project it onto the deviatoric plane \((\rho,
\theta)\) with a fixed value of \(p\).
for i in range(N_loads):
print(f"Loading path#{i}")
dsigma, yielding = sigma_tracing_v(dsigma_path, sigma_n_local)
dp = dsigma @ tr / 3.0 - p
dsigma -= np.outer(dp, derviatoric_axis) # projection on the same deviatoric plane
sigma_returned[i, :] = dsigma
theta_returned[i, :] = Lode_angle_v(dsigma)
rho_returned[i, :] = rho_v(dsigma)
print(f"max f: {jnp.max(yielding)}\n")
sigma_n_local[:] = dsigma
Loading path#0
max f: -2.005661796528811
Loading path#1
max f: -1.6474140052837287
Loading path#2
max f: -1.208026577509537
Loading path#3
max f: -0.7355419142072792
Loading path#4
max f: -0.24734105482689195
Loading path#5
max f: 0.24936204365846004
Loading path#6
max f: 0.5729074243253174
Loading path#7
max f: 0.6673099640326816
Loading path#8
max f: 0.6947128480833946
Then, by knowing the expression of the standrad Mohr-Coulomb yield surface in principle stresses, we can obtain an analogue expression in Haigh-Westergaard coordinates, which leads us to the following equation:
(7)#\[
\frac{\rho}{\sqrt{6}}(\sqrt{3}\cos\theta + \sin\phi
\sin\theta) - p\sin\phi - c\cos\phi= 0.
\]
Thus, we restore the standard Mohr-Coulomb yield surface:
def MC_yield_surface(theta_, p):
"""Restores the coordinate `rho` satisfying the standard Mohr-Coulomb yield
criterion."""
rho = (np.sqrt(2) * (c * np.cos(phi) + p * np.sin(phi))) / (
np.cos(theta_) - np.sin(phi) * np.sin(theta_) / np.sqrt(3)
)
return rho
rho_standard_MC = MC_yield_surface(theta_values, p)
Finally, we plot the yield surface:
colormap = cm.plasma
colors = colormap(np.linspace(0.0, 1.0, N_loads))
fig, ax = plt.subplots(subplot_kw={"projection": "polar"}, figsize=(8, 8))
# Mohr-Coulomb yield surface with apex smoothing
for i, color in enumerate(colors):
rho_total = np.array([])
theta_total = np.array([])
for j in range(12):
angles = j * np.pi / 3 - j % 2 * theta_returned[i] + (1 - j % 2) * theta_returned[i]
theta_total = np.concatenate([theta_total, angles])
rho_total = np.concatenate([rho_total, rho_returned[i]])
ax.plot(theta_total, rho_total, ".", color=color)
# standard Mohr-Coulomb yield surface
theta_standard_MC_total = np.array([])
rho_standard_MC_total = np.array([])
for j in range(12):
angles = j * np.pi / 3 - j % 2 * theta_values + (1 - j % 2) * theta_values
theta_standard_MC_total = np.concatenate([theta_standard_MC_total, angles])
rho_standard_MC_total = np.concatenate([rho_standard_MC_total, rho_standard_MC])
ax.plot(theta_standard_MC_total, rho_standard_MC_total, "-", color="black")
ax.set_yticklabels([])
norm = mcolors.Normalize(vmin=0.1, vmax=0.7 * 9)
sm = plt.cm.ScalarMappable(cmap=colormap, norm=norm)
sm.set_array([])
cbar = fig.colorbar(sm, ax=ax, orientation="vertical")
cbar.set_label(r"Magnitude of the stress path deviator, $\rho$ [MPa]")
plt.show()
Each colour represents one loading path. The circles are associated with the loading during the elastic phase. Once the loading reaches the elastic limit, the circles start outlining the yield surface, which in the limit lay along the standard Mohr-Coulomb one without smoothing (black contour).
Taylor test#
Here, we perform a Taylor test to check that the form \(F\) and its Jacobian \(J\)
are consistent zeroth- and first-order approximations of the residual \(F\). In
particular, the test verifies that the program dsigma_ddeps_vec
obtained by the JAX’s AD returns correct values of the external operator
\(\boldsymbol{\sigma}\) and its derivative \(\boldsymbol{C}_\text{tang}\), which
define \(F\) and \(J\) respectively.
To perform the test, we introduce the operators \(\mathcal{F}: V \rightarrow V^\prime\) and \(\mathcal{J}: V \rightarrow \mathcal{L}(V, V^\prime)\) defined as follows:
\[
\langle \mathcal{F}(\boldsymbol{u}), \boldsymbol{v} \rangle :=
F(\boldsymbol{u}; \boldsymbol{v}), \quad \forall \boldsymbol{v} \in V,
\]
\[
\langle (\mathcal{J}(\boldsymbol{u}))(k\boldsymbol{\delta u}),
\boldsymbol{v} \rangle := J(\boldsymbol{u}; k\boldsymbol{\delta u},
\boldsymbol{v}), \quad \forall \boldsymbol{v} \in V,
\]
where \(V^\prime\) is a dual space of \(V\), \(\langle \cdot, \cdot \rangle\) is the \(V^\prime \times V\) duality pairing and \(\mathcal{L}(V, V^\prime)\) is a space of bounded linear operators from \(V\) to its dual.
Then, by following the Taylor’s theorem on Banach spaces and perturbating the functional \(\mathcal{F}\) in the direction \(k \, \boldsymbol{δu} \in V\) for \(k > 0\), the zeroth and first order Taylor reminders \(r_k^0\) and \(r_k^1\) have the following mesh-independent convergence rates in the dual space \(V^\prime\):
(8)#\[
\| r_k^0 \|_{V^\prime} := \| \mathcal{F}(\boldsymbol{u} + k \,
\boldsymbol{\delta u}) - \mathcal{F}(\boldsymbol{u}) \|_{V^\prime}
\longrightarrow 0 \text{ at } O(k),
\]
(9)#\[
\| r_k^1 \|_{V^\prime} := \| \mathcal{F}(\boldsymbol{u} + k \,
\boldsymbol{\delta u}) - \mathcal{F}(\boldsymbol{u}) - \,
(\mathcal{J}(\boldsymbol{u}))(k\boldsymbol{\delta u}) \|_{V^\prime}
\longrightarrow 0 \text{ at } O(k^2).
\]
In order to compute the norm of an element \(f \in V^\prime\) from the dual space \(V^\prime\), we apply the Riesz representation theorem, which states that there is a linear isometric isomorphism \(\mathcal{R} : V^\prime \to V\), which associates a linear functional \(f\) with a unique element \(\mathcal{R} f = \boldsymbol{u} \in V\). In practice, within a finite subspace \(V_h \subset V\), the Riesz map \(\mathcal{R}\) is represented by the matrix \(\mathsf{L}^{-1}\), the inverse of the Laplacian operator [Kirby, 2010]
\[
\mathsf{L}_{ij} = \int\limits_\Omega \nabla\varphi_i \cdot \nabla\varphi_j \mathrm{d} x , \quad i,j = 1, \dots, n,
\]
where \(\{\varphi_i\}_{i=1}^{\dim V_h}\) is a set of basis function of the space \(V_h\).
If the Euclidean vectors \(\mathsf{r}_k^i \in \mathbb{R}^{\dim V_h}, \, i \in \{0,1\}\) represent the Taylor remainders from (8)–(9) in the finite space, then the dual norms are computed through the following formula [Kirby, 2010]
(10)#\[
\| r_k^i \|^2_{V^\prime_h} = (\mathsf{r}_k^i)^T \mathsf{L}^{-1} \mathsf{r}_k^i, \quad i \in \{0,1\}.
\]
In practice, the vectors \(\mathsf{r}_k^i\) are defined through the residual vector \(\mathsf{F} \in \mathbb{R}^{\dim V_h}\) and the Jacobian matrix \(\mathsf{J} \in \mathbb{R}^{\dim V_h\times\dim V_h}\)
(11)#\[
\mathsf{r}_k^0 = \mathsf{F}(\mathsf{u} + k \, \mathsf{\delta u}) - \mathsf{F}(\mathsf{u}) \in \mathbb{R}^n,
\]
(12)#\[
\mathsf{r}_k^1 = \mathsf{F}(\mathsf{u} + k \, \mathsf{\delta u}) -
\mathsf{F}(\mathsf{u}) - \, \mathsf{J}(\mathsf{u}) \cdot k\mathsf{\delta
u} \in \mathbb{R}^n,
\]
where \(\mathsf{u} \in \mathbb{R}^{\dim V_h}\) and \(\mathsf{\delta u} \in \mathbb{R}^{\dim V_h}\) represent dispacement fields \(\boldsymbol{u} \in V_h\) and \(\boldsymbol{\delta u} \in V_h\).
Now we can proceed with the Taylor test implementation. Let us first start with defining the Laplace operator.
L_form = fem.form(ufl.inner(ufl.grad(u_hat), ufl.grad(v)) * ufl.dx)
L = fem.petsc.assemble_matrix(L_form, bcs=bcs)
L.assemble()
Riesz_solver = PETSc.KSP().create(domain.comm)
Riesz_solver.setType("preonly")
Riesz_solver.getPC().setType("lu")
Riesz_solver.setOperators(L)
y = fem.Function(V, name="Riesz_representer_of_r") # r - a Taylor remainder
Now we initialize main variables of the plasticity problem.
# Reset main variables to zero including the external operators values
sigma_n.x.array[:] = 0.0
sigma.ref_coefficient.x.array[:] = 0.0
J_external_operators[0].ref_coefficient.x.array[:] = 0.0
# Reset the values of the consistent tangent matrix to elastic moduli
Du.x.array[:] = 1.0
evaluated_operands = evaluate_operands(F_external_operators)
_ = evaluate_external_operators(J_external_operators, evaluated_operands)
Inner Newton summary:
Unique number of iterations: [1]
Counts of unique number of iterations: [3750]
Maximum f: -2.2109628558533108
Maximum residual: 0.0
As the derivatives of the constitutive model are different for elastic and plastic phases, we must consider two initial states for the Taylor test. For this reason, we solve the problem once for a certain loading value to get the initial state close to the one with plastic deformations but still remain in the elastic phase.
i = 0
load = 2.0
q.value = load * np.array([0, -gamma])
Du.x.array[:] = 1e-8
if MPI.COMM_WORLD.rank == 0:
print(f"Load increment #{i}, load: {load}")
problem.solve()
u.x.petsc_vec.axpy(1.0, Du.x.petsc_vec)
u.x.scatter_forward()
sigma_n.x.array[:] = sigma.ref_coefficient.x.array
Du0 = np.copy(Du.x.array)
sigma_n0 = np.copy(sigma_n.x.array)
Load increment #0, load: 2.0
Inner Newton summary:
Unique number of iterations: [1]
Counts of unique number of iterations: [3750]
Maximum f: -2.210962855861672
Maximum residual: 0.0
0 SNES Function norm 5.506494297258e-02
Inner Newton summary:
Unique number of iterations: [1]
Counts of unique number of iterations: [3750]
Maximum f: -0.754479660018216
Maximum residual: 0.0
1 SNES Function norm 2.938553015478e-14
If we take into account the initial stress state sigma_n0 computed in the cell
above, we perform the Taylor test for the plastic phase, otherwise we stay in
the elastic one.
Finally, we define the function perform_Taylor_test, which returns the norms
of the Taylor reminders in dual space (10)–(12).
k_list = np.logspace(-2.0, -6.0, 5)[::-1]
def perform_Taylor_test(Du0, sigma_n0):
# r0 = F(Du0 + k*δu) - F(Du0)
# r1 = F(Du0 + k*δu) - F(Du0) - k*J(Du0)*δu
Du.x.array[:] = Du0
sigma_n.x.array[:] = sigma_n0
evaluated_operands = evaluate_operands(F_external_operators)
((_, sigma_new),) = evaluate_external_operators(J_external_operators, evaluated_operands)
sigma.ref_coefficient.x.array[:] = sigma_new
F0 = fem.petsc.assemble_vector(F_form) # F(Du0)
F0.ghostUpdate(addv=PETSc.InsertMode.ADD, mode=PETSc.ScatterMode.REVERSE)
fem.set_bc(F0, bcs)
J0 = fem.petsc.assemble_matrix(J_form, bcs=bcs)
J0.assemble() # J(Du0)
Ju = J0.createVecLeft() # Ju = J0 @ u
δu = fem.Function(V)
δu.x.array[:] = Du0 # δu == Du0
zero_order_remainder = np.zeros_like(k_list)
first_order_remainder = np.zeros_like(k_list)
for i, k in enumerate(k_list):
Du.x.array[:] = Du0 + k * δu.x.array
evaluated_operands = evaluate_operands(F_external_operators)
((_, sigma_new),) = evaluate_external_operators(J_external_operators, evaluated_operands)
sigma.ref_coefficient.x.array[:] = sigma_new
F_delta = fem.petsc.assemble_vector(F_form) # F(Du0 + h*δu)
F_delta.ghostUpdate(addv=PETSc.InsertMode.ADD, mode=PETSc.ScatterMode.REVERSE)
fem.set_bc(F_delta, bcs)
J0.mult(δu.x.petsc_vec, Ju) # Ju = J(Du0)*δu
Ju.scale(k) # Ju = k*Ju
r0 = F_delta - F0
r1 = F_delta - F0 - Ju
Riesz_solver.solve(r0, y.x.petsc_vec) # y = L^{-1} r0
y.x.scatter_forward()
zero_order_remainder[i] = np.sqrt(r0.dot(y.x.petsc_vec)) # sqrt{r0^T L^{-1} r0}
Riesz_solver.solve(r1, y.x.petsc_vec) # y = L^{-1} r1
y.x.scatter_forward()
first_order_remainder[i] = np.sqrt(r1.dot(y.x.petsc_vec)) # sqrt{r1^T L^{-1} r1}
return zero_order_remainder, first_order_remainder
print("Elastic phase")
zero_order_remainder_elastic, first_order_remainder_elastic = perform_Taylor_test(Du0, 0.0)
print("Plastic phase")
zero_order_remainder_plastic, first_order_remainder_plastic = perform_Taylor_test(Du0, sigma_n0)
Elastic phase
Inner Newton summary:
Unique number of iterations: [1]
Counts of unique number of iterations: [3750]
Maximum f: -0.754479660018216
Maximum residual: 0.0
Inner Newton summary:
Unique number of iterations: [1]
Counts of unique number of iterations: [3750]
Maximum f: -0.7544777931845448
Maximum residual: 0.0
Inner Newton summary:
Unique number of iterations: [1]
Counts of unique number of iterations: [3750]
Maximum f: -0.7544609916686915
Maximum residual: 0.0
Inner Newton summary:
Unique number of iterations: [1]
Counts of unique number of iterations: [3750]
Maximum f: -0.7542929752409684
Maximum residual: 0.0
Inner Newton summary:
Unique number of iterations: [1]
Counts of unique number of iterations: [3750]
Maximum f: -0.7526126841444585
Maximum residual: 0.0
Inner Newton summary:
Unique number of iterations: [1]
Counts of unique number of iterations: [3750]
Maximum f: -0.7357971890466226
Maximum residual: 0.0
Plastic phase
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3748 2]
Maximum f: 1.1914324503846294
Maximum residual: 5.037134977947157e-10
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3748 2]
Maximum f: 1.191434439616415
Maximum residual: 5.037159079560956e-10
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3748 2]
Maximum f: 1.1914523427045762
Maximum residual: 5.037359065504066e-10
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3748 2]
Maximum f: 1.1916313737948552
Maximum residual: 5.039395879036141e-10
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3748 2]
Maximum f: 1.1934217055527925
Maximum residual: 5.059805134338341e-10
Inner Newton summary:
Unique number of iterations: [1 3]
Counts of unique number of iterations: [3748 2]
Maximum f: 1.211327098969814
Maximum residual: 5.266651628781508e-10
fig, axs = plt.subplots(1, 2, figsize=(10, 5))
axs[0].loglog(k_list, zero_order_remainder_elastic, "o-", label=r"$\|r_k^0\|_{V^\prime}$")
axs[0].loglog(k_list, first_order_remainder_elastic, "o-", label=r"$\|r_k^1\|_{V^\prime}$")
annotation.slope_marker((2e-4, 5e-5), 1, ax=axs[0], poly_kwargs={"facecolor": "tab:blue"})
axs[0].text(0.5, -0.2, "(a) Elastic phase", transform=axs[0].transAxes, ha="center", va="top")
axs[1].loglog(k_list, zero_order_remainder_plastic, "o-", label=r"$\|r_k^0\|_{V^\prime}$")
annotation.slope_marker((2e-4, 5e-5), 1, ax=axs[1], poly_kwargs={"facecolor": "tab:blue"})
axs[1].loglog(k_list, first_order_remainder_plastic, "o-", label=r"$\|r_k^1\|_{V^\prime}$")
annotation.slope_marker((2e-4, 5e-13), 2, ax=axs[1], poly_kwargs={"facecolor": "tab:orange"})
axs[1].text(0.5, -0.2, "(b) Plastic phase", transform=axs[1].transAxes, ha="center", va="top")
for i in range(2):
axs[i].set_xlabel("k")
axs[i].set_ylabel("Taylor remainder norm")
axs[i].legend()
axs[i].grid()
plt.tight_layout()
plt.show()
first_order_rate = np.polyfit(np.log(k_list), np.log(zero_order_remainder_elastic), 1)[0]
second_order_rate = np.polyfit(np.log(k_list), np.log(first_order_remainder_elastic), 1)[0]
print(f"Elastic phase:\n\tthe 1st order rate = {first_order_rate:.2f}\n\tthe 2nd order rate = {second_order_rate:.2f}")
first_order_rate = np.polyfit(np.log(k_list), np.log(zero_order_remainder_plastic), 1)[0]
second_order_rate = np.polyfit(np.log(k_list[1:]), np.log(first_order_remainder_plastic[1:]), 1)[0]
print(f"Plastic phase:\n\tthe 1st order rate = {first_order_rate:.2f}\n\tthe 2nd order rate = {second_order_rate:.2f}")
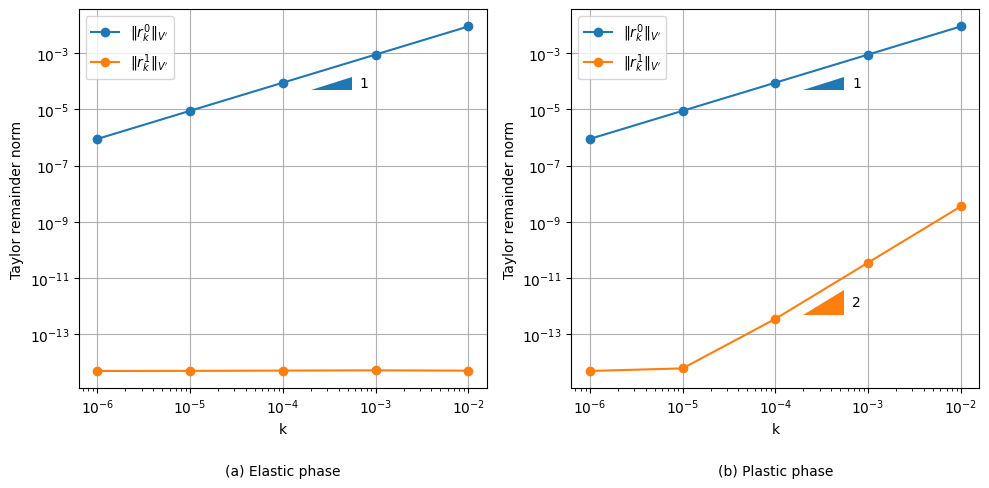
Elastic phase:
the 1st order rate = 1.00
the 2nd order rate = 0.00
Plastic phase:
the 1st order rate = 1.00
the 2nd order rate = 1.93
For the elastic phase (a) the zeroth-order Taylor remainder \(r_k^0\) achieves the first-order convergence rate, whereas the first-order remainder \(r_k^1\) is computed at the level of machine precision due to the constant Jacobian. Similarly to the elastic flow, the zeroth-order Taylor remainder \(r_k^0\) of the plastic phase (b) reaches the first-order convergence, whereas the first-order remainder \(r_k^1\) achieves the second-order convergence rate, as expected.